はじめに
本投稿ではNeural Network LibrariesのPython APIのnnablaパッケージにおいて、独自に任意のForward計算とBackward計算をPython側から定義可能なPythonFunctionという機能を紹介します。
内容のレベルとしては、ある程度ディープラーニングでの学習に慣れ独自の工夫を入れられる中級者からトップレベルの研究者を想定しています。
PythonFunctionは以下のケースで非常に便利です。
- nnablaにレイヤーの実装がなく、複数の関数の組み合わせを使っても定義するのが困難な処理がある
- 解析的な勾配計算定義を使わず、独自のBackward計算を記述したい
以下では、nnablaのレイヤー関数のおさらいを行ったあとに、PythonFunctionの定義の方法を解説し、実用的な例を複数紹介します。
nnablaのレイヤー関数:functions
計算グラフによる実行
まずはじめに、nnablaのレイヤー関数についておさらいします。
nnablaではディープラーニングの学習に用いる自動微分機能を持つ関数の実装がnnabla.functionsパッケージとして公開されています。
使い方は以下の通りです。まずは、計算グラフを定義してForward計算を実行します。
import nnabla as nn
import nnabla.functions as F
import numpy as np
rng = np.random.RandomState(1223)
# 自動微分用の入力変数を定義
x = nn.Variable.from_numpy_array(rng.randn(2, 3),
need_grad=True)
# 関数グラフをnnabla.functionsを使って定義
y = F.relu(x)
z = y * 0.1
# 計算グラフを実行し、表示する
z.forward()
print('x')
print(x.d)
print('y')
print(y.d)
print('z')
print(z.d)
x
[[-1.24733207 0.10773472 -0.9327482 ]
[ 0.37629927 0.59516425 -0.40590292]]
y
[[0. 0.10773472 0. ]
[0.37629926 0.59516424 0. ]]
z
[[0. 0.01077347 0. ]
[0.03762993 0.05951643 0. ]]
nnablaで利用可能なSimpleGraphの機能を用いて、計算グラフを描画してみます。
from nnabla.experimental.viewers import SimpleGraph
SimpleGraph().create_graphviz_digraph(z)
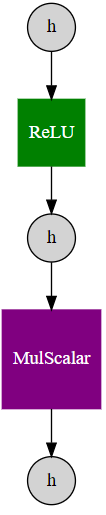
つづいて、Backward計算を実行します。
# 入力変数(パラメタなどの変数の勾配領域を初期化しておく)
x.grad.zero()
# Backward
z.backward()
print('dy(0.1 * x の微分は0.1)')
print(y.g)
print('dx(ReLUの微分は入力が正の要素にだけ伝搬される)')
print(x.g)
dy(0.1 * x の微分は0.1)
[[0.1 0.1 0.1]
[0.1 0.1 0.1]]
dx(ReLUの微分は入力が正の要素にだけ伝搬される)
[[0. 0.1 0. ]
[0.1 0.1 0. ]]
NdArrayによるImperativeな実行
自動微分が不要な場合はNdArrayを使って、numpyの計算を実行するようにForward計算だけ実行可能です。
Variable変数による計算定義とは異なり、nnabla.functionsの関数を呼び出すと、forward計算がすぐに計算が実行されます。
また、計算グラフ自体もつくられません。
print(type(x.data))
y_data = F.relu(x.data)
print(x.data.data)
print(y_data.data)
[[-1.24733207 0.10773472 -0.9327482 ]
[ 0.37629927 0.59516425 -0.40590292]]
[[0. 0.10773472 0. ]
[0.37629926 0.59516424 0. ]]
CUDAのバックエンドを指定すれば、すぐにGPUによる高速な計算も可能です。(以下の例だとわかりにくいですが、GPUで計算が実行されています。)
from nnabla.ext_utils import get_extension_context
nn.set_default_context(get_extension_context('cudnn'))
y_data = F.relu(x.data)
print(y_data.data)
2019-03-20 16:58:43,790 [nnabla][INFO]: Initializing CUDA extension...
2019-03-20 16:58:43,794 [nnabla][INFO]: Initializing cuDNN extension...
[[0. 0.10773472 0. ]
[0.37629926 0.59516424 0. ]]
PythonFunctionによるレイヤー関数の定義
上で紹介したnnabla.functionsに公開されているレイヤー関数はforward計算およびbackward計算がC++およびCUDAで実装されています。
もし、新しい定義を追加したい場合は、C++およびCUDAで関数実装を追加し、ライブラリとPythonパッケージをビルドする必要がありますが、
それは、ほとんどのユーザーにとってはやりたくない作業です。
PythonFunctionでは以下のようにPythonだけで簡単に定義を追加することが可能です。
配列の要素を定数倍するだけのレイヤーの定義
ここでは、簡単な例を見せるため、多次元配列の要素を定数倍するだけというレイヤー関数を定義します。
from nnabla.function import PythonFunction
class PyMulScalar(PythonFunction):
def __init__(self, coef=1.0):
self.coef = coef
@property
def name(self):
return "PyMulScalar"
def min_outputs(self):
return 1
def setup_impl(self, inputs, outputs):
outputs[0].reset_shape(inputs[0].shape, True)
def forward_impl(self, inputs, outputs):
outputs[0].d = self.coef * inputs[0].d
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if propagate_down[0]:
inputs[0].g += self.coef * outputs[0].g
上記コードについては後ほど説明しますが、実行するには以下の通りにクラスをインスタンス化し、
通常のnnabla.functionsと同様にVariableかNdArrayを入力するとグラフが構築できます。
ここでは、2倍する例のため、クラスのコンストラクタに2を指定しました。
実行結果をnumpy.allcloseを使って比較すると正しく2倍したものが出力されていることがわかります。
pymul = PyMulScalar(2)
y = pymul(x)
y.forward()
print(np.allclose(y.d, x.d * 2))
True
計算グラフを見てみます。Callbackという名前の関数になっていることがわかりますが、これはPythonで定義した命令をコールバックの形で呼び出しすのに、nnablaのC++側で実装されているCallbackというレイヤー関数を用いているためです。
SimpleGraph().create_graphviz_digraph(y)

つづいてBackward計算を実行します。nnablaにすでに実装のある掛け算オペレータで行った場合と結果が一致していることが確認できます。
x.grad.zero() # 初期化
y.backward()
print(x.g)
# nnabla.functionsの実装と比較
dx_pf = x.g.copy()
y2 = x * 2
y2.forward()
x.grad.zero()
y2.backward()
print(x.g)
print(np.allclose(x.g, dx_pf))
[[2. 2. 2.]
[2. 2. 2.]]
[[2. 2. 2.]
[2. 2. 2.]]
True
PythonFunction定義の解説
以下に定義部分を再掲します。
PythonFunctionを定義するにはnnabla.functionモジュールからPythonFunctionをインポートして、
クラスを継承して必要なメソッドを実装していきます。
from nnabla.function import PythonFunction
class PyMulScalar(PythonFunction):
def __init__(self, coef=1.0):
self.coef = coef
@property
def name(self):
return "PyMulScalar"
def min_outputs(self):
return 1
def setup_impl(self, inputs, outputs):
outputs[0].reset_shape(inputs[0].shape, True)
def forward_impl(self, inputs, outputs):
outputs[0].d = self.coef * inputs[0].d
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if propagate_down[0]:
inputs[0].g += self.coef * outputs[0].g
__init__
コンストラクタ(イニシャライザ)では定数倍のための係数をクラスメンバとして保持します。普通のクラスであるので、任意のPythonの変数を格納できます。
def __init__(self, coef=1.0):
self.coef = coef
name
nameプロパティでは名前を指定します。
@property
def name(self):
return "PyMulScalar"
min_outputs
min_outputsメソッドでは出力Variable数を指定します。今回は出力を一つしか取らないので、1とします。
def min_outputs(self):
return 1
setup_impl
setup_implメソッドでは必ず出力の配列サイズをresetしてします。
inputs、outputsはそれぞれVariableのリストを格納しており、この関数では入力1つ、出力1つとるのでサイズ1のVariableリストをそれぞれ入力として受け取ります。setup_implに渡されたoutputsは初期化されていないため、reset_shape関数を使ってサイズをリセットします。
この関数では、出力のサイズが入力のサイズと同じになるべきなので、入力のサイズを引数にリセットします。
(ここでは、第2引数のTrueはおまじないだと思ってください。)
def setup_impl(self, inputs, outputs):
outputs[0].reset_shape(inputs[0].shape, True)
forward_impl
forward_implでは実際のForward演算を行います。入力はsetup_implと同じです。
ここでは.dアクセサを使うことで、numpy配列として演算を行っています。
self.coefに格納しておいた値を入力Variableから取り出したnumpy配列にかけて出力に代入しています。
def forward_impl(self, inputs, outputs):
outputs[0].d = self.coef * inputs[0].d
少しの最適化
データの読み書き属性がわかっている場合は次のように適切なものを指定するほうが効率がよくなります(nnablaのArrayクラスでは、デバイス間・型間のデータ転送がリクエストに合わせて行われます。そこで読み書き属性を指定すると、不要なデータ転送が行われなくなり、効率的になります。)。
.dアクセサの代わりに、.data.get_data(rw_str)で読み書き属性を指定できます。
outputs[0].data.get_data('w')[...] = \
self.coef * inputs[0].data.get_data('r')
backward_impl
backward_implでは実際のBackward演算を行います。
forward_implの引数に加えて、グラフエンジンから自動で作られて渡される値で、propagate_downとaccumが追加されています。
propagate_down(boolのリスト):入力Variableへの勾配を計算する必要があるかを指すaccum(boolのリスト):入力Variableへの勾配の計算結果を足し込む(accumulate)べきかどうか。Trueの場合は+=で計算結果の勾配をaccumulateする必要がある。、Falseの場合は=代入を使うことが可能である。
以下の通り、accumオプションは無視することが可能で、常に+=で結果を.gに加算しておけば常に正しい計算をしていることとなります。
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if propagate_down[0]:
inputs[0].g += self.coef * outputs[0].g
少しの最適化
読み書き属性を付加することでより効率的に不要なデータ転送を避けたい場合は、
以下のように書くことができます。
if propagate_down[0]:
tmp = self.coef * outputs[0].grad.get_data('r')
if accum[0]:
inputs[0].grad.get_data('rw') += tmp
else:
inputs[0].grad.get_data('w')[...] = tmp
CUDAなどのBackendを利用可能にする定義
PythonFunctionにおいても上記で解説したNdArrayによるImperativeな実行が可能です。Imperativeな実行においてはnnabla.set_default_contextまたはnnabla.context_scopeで指定されているバックエンドデバイスによる実行なため、CUDAなどGPUを用いたバックエンドを利用した高速な実行が可能となります。
実際に以下のように書くことが可能です。
class PyMulScalar2(PythonFunction):
def __init__(self, coef=1.0):
self.coef = coef
@property
def name(self):
return "PyMulScalar"
def min_outputs(self):
return 1
def setup_impl(self, inputs, outputs):
outputs[0].reset_shape(inputs[0].shape, True)
def forward_impl(self, inputs, outputs):
outputs[0].data.copy_from(self.coef * inputs[0].data)
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if propagate_down[0]:
tmp = self.coef * outputs[0].grad
grad = inputs[0].grad
if accum[0]:
grad += tmp
else:
grad.copy_from(tmp)
先程の例と同様に以下の通りに実行が可能です。
pymul2 = PyMulScalar2(2)
y = pymul2(x)
y.forward()
x.grad.zero()
y.backward()
print(y.d)
print(np.allclose(y.d, x.d * 2))
print(x.g)
[[-2.4946642 0.21546943 -1.8654964 ]
[ 0.7525985 1.1903285 -0.81180584]]
True
[[2. 2. 2.]
[2. 2. 2.]]
numpyを用いた場合とnnablaのImperative計算の場合の計算時間を計測して比較してみます。
x_large = nn.Variable.from_numpy_array(
rng.randn(64, 3, 224, 224).astype(np.float32))
y_large = pymul(x_large)
y_large2 = pymul2(x_large)
まずは、numpyの場合の計算時間をみます。(以下ではIPythonの%%マジックコマンド%%timeitを利用しています。実行の際はIPythonやJupyterなどを使ってください。)
%%timeit -n 10 -r 5
y_large.forward()
y_large.backward()
20.9 ms ± 3.25 ms per loop (mean ± std. dev. of 5 runs, 10 loops each)
続いて、imperative実行の計算時間を計測します。
# CUDAの演算は非同期に行われるため、
# バックエンドモジュールの`device_synchronize`関数で同期する
from nnabla.ext_utils import import_extension_module
cuda = import_extension_module('cudnn')
%%timeit -n 10 -r 5
y_large2.forward()
y_large2.backward()
cuda.device_synchronize('0')
1.29 ms ± 465 µs per loop (mean ± std. dev. of 5 runs, 10 loops each)
以上の計測の通り、Imperative実行の場合に約10倍高速化されていることが確認できました。
実用的なPythonFunctionの例
ここまでは概要を理解するために配列の値を定数倍するだけであまり有用ではない例を見てきました。ここでは、より実用的な例を見ていきます。
GradientReversal
ここでは、Unsupervised Domain Adaptation by Backpropagationという論文で用いられるGradient reversal layerというレイヤーを紹介します。
この論文では、学習データとテスト環境のデータの性質が異なるドメインシフト問題を扱っています。この問題に対応することをドメイン適合(Domain Adaptation)と呼びます。
この論文で提案する手法では、学習用データ・セットではカテゴリラベルの分類誤差を最小化しつつ、(ラベルのついていない)異なるドメインのデータを分類する誤差を最大化します。学習されるディープモデルにより抽出される特徴量はドメインの変化に不変的なものとなり、新しいドメインでも分類性能の高いモデルになるという仕掛けです。その中で出てくるGradient reversal layerでは、勾配の符号を挿入したレイヤーで逆転させることで、ロス関数で用いていたことと逆方向への最適化をしています。下図のようにドメイン分類性能はピンクの領域では最大化しつつ、緑の領域ではドメイン分類性能を下げることでドメイン不変な特徴量を学習させます。
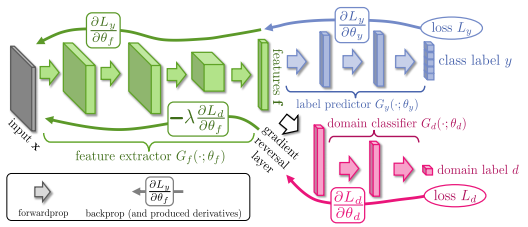
レイヤーの定義は以下のようになります。
def _grad(lhs, rhs, accum):
'''accumによる処理の分岐をよく使うので関数にしておく'''
if accum:
lhs += rhs
else:
lhs.copy_from(rhs)
class GradientReversalLayer(PythonFunction):
def __init__(self):
pass
@property
def name(self):
return "GradientReversalLayer"
def min_outputs(self):
return 1
def setup_impl(self, inputs, outputs):
outputs[0].reset_shape(inputs[0].shape, True)
def forward_impl(self, inputs, outputs):
outputs[0].data.copy_from(inputs[0].data)
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if not propagate_down[0]:
return
_grad(inputs[0].grad, -outputs[0].grad, accum[0])
以下のように、Gradient reversal layerにより勾配の符号が反転していることが確認できます。
x = nn.Variable.from_numpy_array(
np.asarray([1], dtype=np.float32), need_grad=True)
y = GradientReversalLayer()(x)
y.forward()
print(y.d)
x.grad.zero()
y.backward()
print(x.g)
[1.]
[-1.]
ShakeShake
ここでは、Shake-Shake regularizationという手法で使われている乱数によるレイヤーを紹介します。
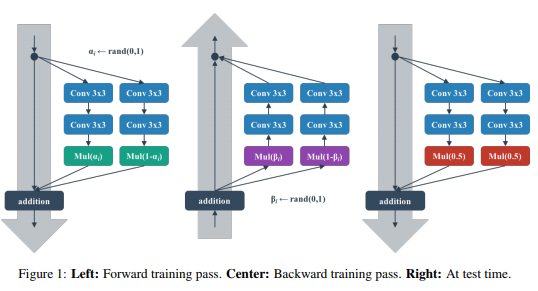
この手法では、学習中にランダムにノイズを入れることで新しいデータで性能を向上させるテクニックの一つとして、Shake-Shakeというノイズ付加の方法を提案しています。具体的には、2つの異なるパスからくるVariableをある係数をかけてブレンドする処理を考えたときに、このブレンドの比率を各forward計算時に乱数でサンプルされた比率aでブレンドします。さらに、forward計算時だけでなく、backwardでも異なる乱数による比率bを用いてブレンドします。(テスト時には平均値でブレンドしますがここでは扱いません。)
このため、backward計算はforward計算の解析的な勾配計算とはなっていないため、既存のレイヤーの組み合わせでは記述できない処理となっています。
実装例は以下の通りです。
class ShakeShake(PythonFunction):
def __init__(self, rng=None):
if rng is None:
rng = np.random.RandomState(1223)
self.rng = rng
@property
def name(self):
return "ShakeShake"
def min_outputs(self):
return 1
def setup_impl(self, inputs, outputs):
assert len(inputs) == 2
assert inputs[0].shape == inputs[1].shape
outputs[0].reset_shape(inputs[0].shape, True)
def forward_impl(self, inputs, outputs):
# sample blending coefficient
a = self.rng.rand()
print('Debug: a={}'.format(a))
outputs[0].data.copy_from(
a * inputs[0].data + (1 - a) * inputs[1].data)
def backward_impl(self, inputs, outputs,
propagate_down, accum):
if not any(propagate_down):
return
b = self.rng.rand()
print('Debug: b={}'.format(b))
ratio = [b, 1 - b]
for i in range(2):
if propagate_down[i]:
_grad(inputs[i].grad,
ratio[i] * outputs[0].grad, accum[i])
使ってみます。簡単のため、サイズが1のアレイを入力としてそれぞれ1, 2の値を入れておきます。
x0 = nn.Variable.from_numpy_array(
np.asarray([1], dtype=np.float32), need_grad=True)
x1 = nn.Variable.from_numpy_array(
np.asarray([2], dtype=np.float32), need_grad=True)
y = ShakeShake()(x0, x1)
実行すると1回目のforwardでは\(a = 0.529…\)となるが、これに従い計算した結果、\(a \times 1 + (1 – a) \times 2 = 1.4709…\)となり結果が一致していることが確認できます。
y.forward()
print(y.d)
Debug: a=0.5290767986417101
[1.4709232]
backwardを実行してみます。以下のデバッグログから手計算すると勾配の結果が一致していることが確認できます。
x0.grad.zero()
x1.grad.zero()
y.backward()
print(x0.g)
print(x1.g)
Debug: b=0.16335436356818256
[0.16335437]
[0.83664566]
まとめ
本投稿ではnnablaの提供するPythonFunctionによる独自レイヤー定義方法を紹介しました。はじめにも述べた通り、PythonFunctionは以下のケースで非常に有用です。
- nnablaにレイヤーの実装がなく、複数の関数の組み合わせを使っても定義するのが困難な処理がある
- 解析的な勾配計算定義を使わず、独自のBackward計算を記述したい
特に、最もユースケースの多い2番目の点についてはいくつか実用的な例を紹介しました。
1番目のユースケースについては紹介はしませんでしたが、実用的な例として、様々な最先端手法の学習コードを取り揃えているnnabla-examplesリポジトリの物体検出モデルYOLOv2のスクリプト内でforward計算途中の動的な正解ラベルの生成にこのPythonFunctionを利用しています。