ニューラルネットワークの学習のしくみ
ニューラルネットワークの学習とは、ネットワークが内部で行う演算に用いるパラメータをより良いものに更新していく作業といえます。
基本的なニューラルネットワークの学習には、入力データと、それに対する出力として「正しい」データ、すなわち教師データが必要ですが、これはニューラルネットワークの学習が以下のような反復的なプロセスによって構成されているからです。
- 入力データと現在のパラメータから出力値を出力
- 出力値と正解データとの「誤差」を算出
- 誤差を減少させるようにパラメータを更新する
2で算出される「誤差」ですが、これは入力データに対し、現在のニューラルネットワークの出力値が実際の出力(正解)とどれくらい離れているかを意味します。
そしてこの「誤差」が十分小さくなるまで上記のプロセスを反復させることで、ニューラルネットワークの学習を実現していきます。「誤差」が小さくなることはすなわち、ニューラルネットワークが入力に対し正解に「限りなく近い」出力を出すようになったと言い換えることができるからです。
このように、誤差を最小化させていくことで解くことができる問題の例として、線形回帰問題を考えてみましょう。
パラメータ\(a, b\)に対し入力データ\(x\)と正解データ\(Y\)があるとき、予測される回帰直線の式は\(y=ax+b\)と表せます(さらに、パラメータの真値をそれぞれ\(A, B\)とすれば\(Y=Ax+B\)と表せます)。
ここで、同じ\(x\)に対しても異なる値の\(a\)と\(b\)を用いることで出力値\(y\)は変化し、予測される回帰直線は異なるものになります。\(a\)と\(b\)がランダムな値をとるとき、予測される回帰直線はあてずっぽうのようなものです。図1がそれにあたります。
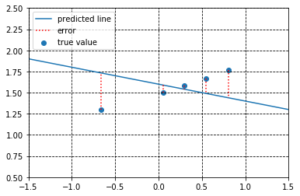
図1. パラメータが適切でない回帰直線。
ニューラルネットワークによってこの回帰直線を予測する問題を考えたとき、学習が進んでいない時点でのニューラルネットワークの出力がこれにあたります。
しかしながら、前述したように\(a\)と\(b\)の値を更新していくことで、予測される回帰直線を真の回帰直線に近づけることができます(図2参照)。ここで、予測値\(y\)と真値\(Y\)の「距離」を「誤差」とみなし(これが2で行われるプロセスです )、この「誤差」を小さくするように\(a\)と\(b\)の値を更新していきます。一度あたりの更新で修正される「誤差」はわずかかもしれませんが、何度も行うことで「誤差」は小さくなっていくことが予想されます。
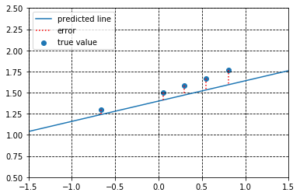
図2. パラメータを調整することにより、出力が真値に近づいた回帰直線。
これを繰り返すことで、予測値である出力\(y\)が入力に対し正解\(Y\)と大差ない値となってくることが期待されます。この線形回帰問題をニューラルネットワークによる回帰直線の予測問題とみなせば、ここで行われたパラメータ\(a, b\)の更新こそがニューラルネットワークの「学習」に相当します。
多くのディープラーニングフレームワークにはこのプロセスを自動で行ってくれる機能があります。Neural Network LibrariesにおいてはSolverがその役目を果たします。そして、このSolverを利用する際に重要な概念として、勾配(gradient)があります。ここでは、上に挙げた線形回帰問題を例にとり、Neural Network LibrariesにおけるSolverと勾配の使い方を見ていきたいと思います。
計算グラフを構築する
import matplotlib.pyplot as plt
import nnabla as nn
import nnabla.functions as F
import numpy as np
まずは必要なライブラリをインポートします。
次に、解きたい線形回帰問題の答えとなる関数をあらかじめ作ってしまいます(ここでは、求めたい回帰直線の式は\(Y=0.3x+1.5\)とします。)
入力となるVariableである\(x\)と、正解出力となるVariableである\(y_{true}\)を用意します。
未知の回帰直線における傾きおよび切片をそれぞれ\(a\)と\(b\)というVariableで作成します。
学習によって求めたいパラメータはこの\(a\)と\(b\)なので、今回はこれらをnn.parameter.get_parameter_or_create()を用いて作成しておきます。
なお、この記事においては学習パラメータをこのように作成しますが、これは特殊なケースであることに注意してください。
Neural Network Librariesでは、nnabla.parametric_functionsを用いることで学習パラメータの作成を意識することなく計算グラフを構築していくことができます。
batch_size = 32
A, B = 0.3, 1.5
x = nn.Variable((batch_size, 1))
y_true = nn.Variable((batch_size, 1))
a = nn.parameter.get_parameter_or_create("a", (1,1), need_grad=True)
b = nn.parameter.get_parameter_or_create("b", (1,1), need_grad=True)
nn.get_parameters()
ここでbatch_sizeはネットワークに一度に与えるデータの個数です。今回は一度に32個のデータ群を与えます(つまり1バッチに32個のデータが含まれる)。
nn.get_parameters()を使うことでパラメータが作成されているか確認できます。
OrderedDict([('a', <Variable((1, 1), need_grad=True) at 0x7fe4f646e5e8>),
('b', <Variable((1, 1), need_grad=True) at 0x7fe4f646e548>)])
これらを用いると、予測したい回帰直線は\(y=ax+b\)と表すことができ、実際にその計算グラフを作ります。同時に、予測と実際の正解との誤差をまとめた損失関数と呼ばれるものを定義します。今回は、損失関数を入力データ群と正解データ群の誤差の二乗和の平均とします。これを最小化するような\(a\)と\(b\)を求めるのが今回の目的、すなわちニューラルネットワークを用いた回帰直線の予測です。
y = F.add2(F.mul2(a,x), b)
loss = F.mean(F.pow_scalar(F.sub2(y_true, y), 2))
入力データに対する正解データを作ります。入力として正規分布からサンプリングされた\(X\)を用意し、それに対する真の回帰直線上での対応点、すなわち正解データ\(Y\)を算出します(また、若干の乱数を加えています)。
max_iter = 1000
X = np.random.randn(max_iter*batch_size)
Y = A*X + B + 0.01*np.random.randn(X.size)
Solverの準備
いよいよSolverを定義します。nnabla.solversをインポートし、用いる最適化手法に応じたクラスを呼びます。ここでは、SGD(確率的勾配降下法)を使っていきます。
import nnabla.solvers as S
solver = S.Sgd(0.01)
ここでSGDが受け取っている引数は学習率です。定義が終わったら、次は最適化させたいパラメータ変数をSolverに登録する必要があります。これにはsolver.set_parameters()を使います。
solver.set_parameters(nn.get_parameters())
いよいよ学習を始める準備が整いました。まずは、\(a\)と\(b\)の初期値を決めましょう。ここでは乱数を初期値として与えます。
a.d = np.random.random()
b.d = np.random.random()
print(a.d, b.d)
[[0.5186109]] [[0.32514971]]
初期値が与えられました。
ここで、現在の\(a\)と\(b\)の値をもとに予測された回帰直線と正解データをプロットする関数を定義し、現在どのような予測がなされているか確認してみます。
def show_result(a, b, X, Y, with_info=False, iteration=None, loss=None):
x = np.arange(-5,5)
y = (a.d*np.arange(-5,5))+b.d
y = np.reshape(y, (y.size))
plt.scatter(X[:50],Y[:50])
plt.plot(x, y)
plt.ylim([0.5,2.5])
plt.grid(which='major',color='black',linestyle='dashed')
if with_info:
plt.text(-3.95, 2.30, r'Iter:{}'.format(iteration), size=15)
plt.text(-3.95, 2.05, r'Loss={:.3f}'.format(float(loss.d)), size=15)
plt.text(-3.95, 1.80, r'a={:.3f}'.format(float(a.d)), size=15)
plt.text(-3.95, 1.55, r'b={:.3f}'.format(float(b.d)), size=15)
plt.show()
show_result(a, b, X, Y)
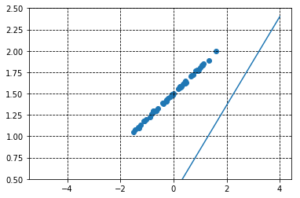
図3. 図1同様、ランダムなパラメータをもつために回帰直線は大きくずれてしまっている。
当然ですが、大きくずれた直線が表示されています。
では、\(a\)と\(b\)の値を学習によって最適化させていくと、どのような直線になっていくか見ていきましょう。まずは、この状態でどれだけ誤差があるかを調べます。ここでは誤差の二乗和平均を損失関数としているので、この損失を算出することと誤差の算出は同義です。\(x\)と\(y_{true}\)にそれぞれ入力値と正解値をセットし、loss.forward()を呼ぶことで現時点での損失関数の値が求まります。
x.d = np.reshape(X[:batch_size], (batch_size, 1))
y_true.d = np.reshape(Y[:batch_size], (batch_size, 1))
loss.forward()
print(loss.d)
1.468268
現時点での誤差がこれくらいであるとわかりました。
勾配(gradient)とパラメータの更新
ニューラルネットワークにおける学習のポイントは、ここで求めたこの誤差をもとに、各変数の勾配と呼ばれる値が導出され、それが計算グラフの上流(すなわち入力)に向かって伝搬していく点にあります。これらの理論的背景は割愛しますが、ここからはNeural Network Librariesにおいてはどのようにこの勾配を算出していくかを見ていきましょう。
print(a.g, b.g)
[[0.00541324]] [[-0.00076724]]
勾配自体はすべてのVariableが持ちうるものです。そのため、すべてのVariableには勾配にアクセスできるメソッドがあります。Variableの値にアクセスできるVariable.dと同様に、Variable.gを用いることで、任意のタイミングで勾配の値を確認することができます。しかしながらVariableの値同様、Variableの定義時には勾配も初期化されていない点には注意が必要です(上の例で表示された勾配は計算によって算出された正しい勾配ではありません)。
勾配の初期化にはsolver.zero_grad()を用います。
solver.zero_grad()
print(a.g, b.g)
[[0.]] [[0.]]
これは初期化というよりも、(Solverに登録された)すべてのVariableの勾配を0にするという点から、勾配のリセットと言ったほうが正しいかもしれません。もちろん、すべてのVariableの勾配の値に対して直接0を代入することでも同じ処理が可能です。
こうして勾配を0に初期化した後、勾配を算出するには、loss.backward()を用います。前もって算出した誤差と計算グラフの構造をもとに、各Variableに対して勾配が算出されます。
loss.backward()
print(a.g, b.g)
[[0.66854817]] [[-2.3782601]]
SGDにおけるパラメータ更新は非常にシンプルであり、現在の値から学習率と勾配の積を引いたものが次の値となります。そのため、現在のパラメータの値と勾配の値、そして学習率がわかれば、次の更新によって値がどう変化するかを理論的に予測することができます。実際に予測値を見てみましょう。
print("Originally, a = {} and b = {}".format(a.d, b.d))
print("Expected Updated Values are a = {} and b = {}".format(a.d - 0.01*a.g, b.d - 0.01*b.g))
Originally, a = [[0.5186109]] and b = [[0.32514971]]
Expected Updated Values are a = [[0.5119254]] and b = [[0.34893233]]
予測された更新後の値は a = 0.5119254, b = 0.34893233でした。
それでは実際にSolverを使ってパラメータの更新を行いましょう。パラメータの更新には、Solverに登録されたパラメータ変数の勾配が算出された状態でSolver.update()を実行します。
solver.update()
print("Updated Values are a = {} and b = {}".format(a.d, b.d))
パラメータ更新後の値をチェックしてみます。
Updated Values are a = [[0.5119254]] and b = [[0.34893233]]
a = 0.5119254, b = 0.34893233となり、理論的に予測された値と一致しました(このことから分かるように、手動でパラメータの更新を行うことも可能ですが、実行速度などの面からSolverの利用を強く推奨します)。
勾配を利用してパラメータを更新した後でも、勾配の値は残ってしまっていることに注意してください。また、再度loss.backward()を実行すると、勾配の値は再度算出され、現在の勾配の値に加算されます。これを利用する事で、勾配を蓄積させていくといったこともできますが、そうでない場合にはsolver.zero_grad()を用いて勾配を0にリセットすることを忘れないようにしましょう。
print(a.g, b.g) # 値は残り続けます
[[0.66854817]] [[-2.3782601]]
また、勾配の値を直接変更することも可能ですが、意図的にこのような操作をしたいとき以外には避けるべきです。ただし、Gradient Clippingなどを利用するときなど、あえてこのような操作が必要になるときもあります。
a.g = 15 # aの勾配の値を15に変更します
b.g = -10 # bの勾配の値を-10に変更します
print("At this moment, a = {} and b = {}".format(a.d, b.d))
print("Expected Updated Values are a = {} and b = {}".format(a.d - 0.01*a.g, b.d - 0.01*b.g))
solver.update() # この状態でパラメータを更新します
print("Updated Values are a = {} and b = {}".format(a.d, b.d))
a.d = a.d + 0.01*a.g # SGDによる更新式をもとに
b.d = b.d + 0.01*b.g # 値の復元を行います
print("Now it's back! a = {} and b = {}".format(a.d, b.d))
At this moment, a = [[0.5119254]] and b = [[0.34893233]]
Expected Updated Values are a = [[0.36192542]] and b = [[0.44893232]]
Updated Values are a = [[0.36192542]] and b = [[0.44893232]]
Now it's back! a = [[0.5119254]] and b = [[0.34893233]]
Solverと勾配についての説明は以上です。これから、冒頭で述べたように線形回帰を行っていきます。
Solverを用いて回帰直線を予測する
200回のパラメータ更新を行い、正解データに適合するような回帰直線を求めていきます。
for i in range(200):
index = np.random.randint(max_iter - 1)
x.d = np.reshape(X[index*batch_size:(index+1)*batch_size], (batch_size, 1))
y_true.d = np.reshape(Y[index*batch_size:(index+1)*batch_size], (batch_size, 1))
loss.forward()
solver.zero_grad()
loss.backward()
solver.update()
if i % 20 == 0:
print("loss: {}".format(loss.d))
print("a: {}, b: {}".format(a.d, b.d))
show_result(a, b, X, Y, True, i, loss)
以下の図が予測されたパラメータと、それらをもとに作成された回帰直線です(20回のパラメータ更新ごとにその時点での予測回帰直線を表示しています)。
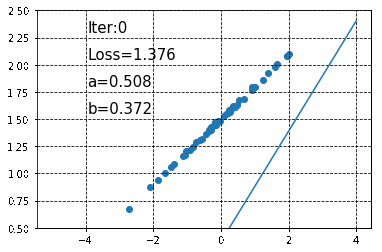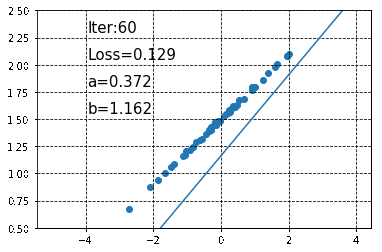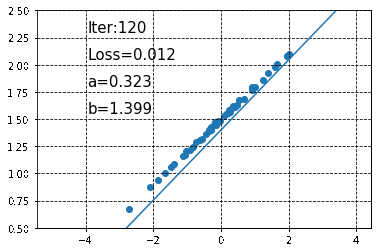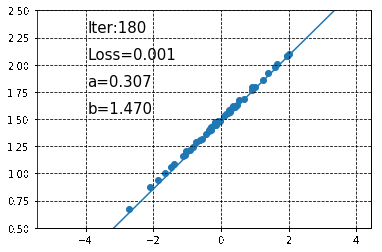
徐々に直線が真の回帰直線に近づいていくのが分かります。また、200回のパラメータ更新が終わった状態で\(a\)と\(b\)の値を見てみると、それぞれa = 0.30450833, b = 1.479325であり、あらかじめ設定した値に非常に近い値になっていることがわかります。なお、この時点で予測される回帰直線は以下のようになります。
show_result(a, b, X, Y, i, loss)
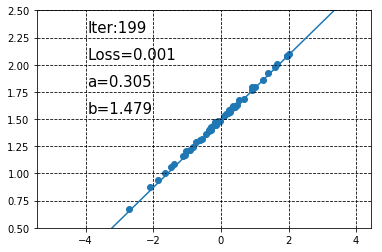
ほとんど正解データと一致する回帰直線が得られました。
Neural Network Librariesには、ここで用いたSGD以外にもMomentumやAdamなど、ディープラーニングで頻繁に用いられる最適化手法が多数用意されています。さらにSolverにはweight decay(重み減衰)や現在登録されているパラメータの確認、学習率調整などに使える機能もついています。
ここでの例は非常に単純なものであり、一般的なディープラーニングの学習とは大きく異なる例を取り上げましたが、基本的なコンセプト・学習プロセスは変わりません。勾配がいつ・どのように使われているかをしっかり理解すれば、複雑なネットワークも難なく書きこなすことができるでしょう。